NOVIEMBRE

1) FUNCIONES REALES DE VARIAS VARIABLES

Son funciones de la forma:

f: R^n =====>  R donde 

(X1,X2,...Xn)    z = f(X1,X2,...Xn)  de n componentes 

En R2 : 

f: R2 =====>  R

(x,y)   z= f(x,y) una funcion en R2

x,y = son las variables independientes

z= es la variable dependiente

Representacion grafica 

Dominio de definicion o campo de existencia

Es el dominio donde f(x,y) existe y es una region del plano XOY o todo el plano XOY

Analisis del dominio de definicion

Para comprender mejor realizaremos un ejemplo

i) Analisis Matematico 

ii) Analisis Grafico

En R2

En R3

iii) Analisis Descriptivo

El dominio son todos los pares (x,y), tales que sean mayores o iguales a la recta y=-1-x siendo x diferente de 1

Curvas de nivel

Las curvas de nivel de una funcion f(x,y), son las curvas cuyas ecuaciones son f(x,y)=k donde "k" es una constante en el rango de f(x,y).

Curvas de Contorno

Son las curvas de nivel representadas en R3

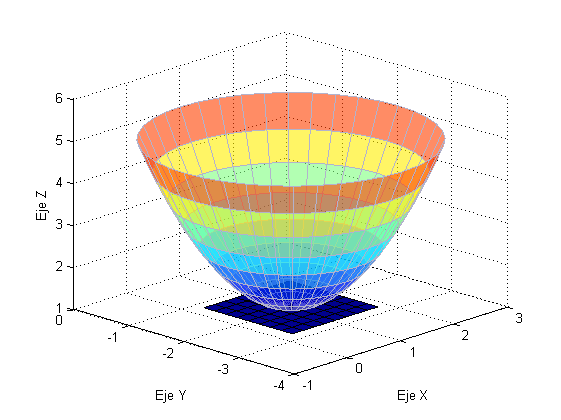
Superficies de Nivel

Si w = f(x,y,z) y w = k, donde k es una constante. K = f(x,y,z

Limites y Continuidad

f: R2 =====>  R

(x,y) ===> z=f(x,y)

Observaciones acerca de la existencia de un límite:

- Si por dos camnios o trayectorias el valor del límite tiene un valor diferente, entonces se concluye que no existe el límite.

- Si por dos o más caminos o trayectorias el valor del límite tiene el mismo valor, se supone que el límite existe y se debe proceder a demostrar su existencia.

-Los caminos elegidos para evaluar el límite deben contener el punto (a,b) de interes

Ejercicios

Continuidad 

Se dice que una función es continua en (a,b) si se cumple:

Esto significa  que tanto la función evaluada en (a,b) debe existir y el limite evaluado en (a,b) también debe existir y deben  de ser iguales. Si no se cumple aliigunas de las condiciones, entonces se dice que f(x,y) es discontinua en (a,b) y puede ser:

i) Discontinua Evitable

ii)Discontinua inevitable

-Toda discontinuidad evitable se puede redifinir

Nota: Las propiedades de los limites de funciones  de una sola variable se aplican tambien para los limites de funciones de dos variables

Ejercicios

2) DERIVADAS PARCIALES

f: R2 =====>  R

(x,y) ===> z=f(x,y)

Las derivadas parciales son las funciones fx y fy definidas por

Observaciones:  

- Cuando derivamos parcailmente con respecto a "x", la variable "y" se asume como constante.

- Cuando derivamos parcailmente con respecto a "y", la variable "x" se asume como constante.

- Se aplican todas las reglas de derivación de la funciones de una variable

Interpretaciones de las derivadas parciales

1. Interpretación geométrica, que se refiere a la pendiente de la recta tangente en el punto (x,y) cuando "x" es fijo (al derivar con respecto a y) o cuando "y" es fijo (al derivar con respecto x).

2. Interpretación física, estas representan las razones de cambio de la variable z =f(x,y) cuando "x" varia manteniendo fija "y" o  cuando "y" varia manteniendo fija "x".

Se puede hablar de tasas o índices de cambio

Planos Tangentes

Supongamos que f(x,y) tiene derivadas parciales de primer orden continuas. Entonces el plano tangente a la superficie z=f(x,y) en el punto P(a,b,f(a,b)) es el plano que pasa por  P que contien las rectas tangentes a las dos curvas.

- El vector normal a este plano tangente será:

                                                                      A            B            C

Por lo tanto la ecuación del plano tangente es:

Ejercicios

Derivadas de orden superior

Si z= f(x,y) entonces existe:

4 derivadas parciales de segundo orden

8 derivadas parciales de tercer orden

2n derivadas parciales de "n" orden

Si w= f(x,y,z) entonces existe:

3n derivadas parciales de "n" orden

Derivadas Cruzadas 

Dxy=Dyx

Se cumple solo si z= f(x,y) es una funcion continua